摘要
控制流 if-else 是每个程序员对编程的第一认识。但既然是复习,补漏还是要认真看一遍。比如像do-while,continue,标签,这些我平时写代码的时候用的不多。但在恰当的情况下,这些控制语句还是能简化一些问题的。
while 和 do-while
//语法
do
statement
while(Boolean-expression);
//栗子
Random dice = new Random(77);
do
System.out.println("爱美,爱智慧");
while(dice.nextInt(100)<99);
和 while 的区别是,do-while的语句至少会被执行一次。之前很少用do-while,以后可以多用用。
练习1
Write a program that prints values from 1 to 100.
//exercise 1: print 1-100
public static void oneToHundred(){
for(int i=1;i<101;i++){
System.out.println(i);
}
}
//output: 1-100
练习2
Write a program that generates 25 random int values. For each value, use an if-else statement to classify it as greater than, less than, or equal to a second randomly generated value.
private Random dice = new Random(77);
//exercise 2: classifier 25 int
public int[] intClassifier(int times){
//result container
int[] resultPool={0,0,0};
for(int i=0;i<times;i++){
int first=this.dice.nextInt(100);
int second=this.dice.nextInt(100);
if(first<second){
resultPool[0]+=1;
} else if(first==second){
resultPool[1]+=1;
} else {
resultPool[2]+=1;
}
}
return resultPool;
}
//output:
//结果数组代表:[当前大于下一个,相等,小于]
//[12, 1, 12]
练习3
Modify Exercise 2 so that your code is surrounded by an “infinite” while loop. It will then run until you interrupt it from the keyboard (typically by pressing Control- C).
private Random dice = new Random(77);
public void autoClassifier(){
//result container
int[] resultPool={0,0,0};
while(true){
int first=this.dice.nextInt(100);
int second=this.dice.nextInt(100);
if(first<second){
resultPool[0]+=1;
} else if(first==second){
resultPool[1]+=1;
} else {
resultPool[2]+=1;
}
System.out.println(Arrays.toString(resultPool));
}
}
output:
//我按ctrl+c的时候,停在了这里
//结果数组代表:[当前大于下一个,相等,小于]
[560789, 11429, 559570]
[560789, 11429, 559571]
[560790, 11429, 559571]
[560790, 11429, 559572]
[560791, 11429, 559572]
[560792, 11429, 559572]
[560793, 11429, 559572]
[560794, 11429, 559572]
练习4
Write a program that uses two nested for loops and the modulus operator (%) to detect and print prime numbers (integral numbers that are not evenly divisible by any other numbers except for themselves and 1).
找素数,素数的定义就是除1和他自己之外,不能被其他正整数整除。基本思路就是让数x从2到x-1都取模 %(就是求余数),余数都不为零,就是素数啦。(要当心2。当然这里没有造成麻烦。)
//exercise 4: prime detector that return all prime number from 1 to the given max number.
public static List<String> primeFilter(int max){
List<String> resultPool=new ArrayList<String>(); //面向接口声明更好
//test every number from 1 to max
for(int currNum=1;currNum<max+1;currNum++){
//currNum is treated as prime number by default
boolean isPrime=true;
int testNum=2;
for(testNum=2;testNum<currNum;testNum++){
//currNum is not prime number
if(currNum%testNum==0){
isPrime=false;
break;
}
}
if (isPrime){
System.out.println("Found "+currNum+" is prime!!!");
resultPool.add(Integer.toString(currNum));
} else {
System.out.println(currNum+" pass!!!");
}
}
return resultPool;
}
output:
//test 1-20
Found 1 is prime!!!
Found 2 is prime!!!
Found 3 is prime!!!
4 pass!!!
Found 5 is prime!!!
6 pass!!!
Found 7 is prime!!!
8 pass!!!
9 pass!!!
10 pass!!!
Found 11 is prime!!!
12 pass!!!
Found 13 is prime!!!
14 pass!!!
15 pass!!!
16 pass!!!
Found 17 is prime!!!
18 pass!!!
Found 19 is prime!!!
20 pass!!!
练习 5
Repeat Exercise 10 from the previous chapter, using the ternary operator and a bitwise test to display the ones and zeroes, instead of Integer.toBinaryString( ).
第三章,练习10:
Write a program with two constant values, one with alternating binary ones and zeroes, with a zero in the least-significant digit, and the second, also alternating, with a one in the least-significant digit (hint: It’s easiest to use hexadecimal constants for this). Take these two values and combine them in all possible ways using the bitwise operators, and display the results using Integer.toBinaryString( ).
这道题比较好玩,我解释一下解题思路:
比如说我们要处理的数字是:170。写成16进制是:aa。写成二进制是:10101010。符合题中要求1,0间隔,最低位是0。在实际32位int内存里,他长这样:00000000000000000000000010101010。
思路是用特殊掩码和这个数做 AND “与”操作。当掩码只有最低位是1的时候,其他位“与”的结果永远是0,只有最低位如果是1的时候,才输出1,此时“与”操作的结果与掩码相同。如果最低位是0,那掩码将被擦除。
00000000000000000000000010101010 //女主角170,最低位为0
00000000000000000000000000000001 //掩码只有最低位是1
--------------------------------
00000000000000000000000000000000 //女主角最低位是0,掩码被擦除
00000000000000000000000101010101 //男主角341,最低位为1
00000000000000000000000000000001
--------------------------------
00000000000000000000000000000001 //男主角最低位是1,掩码被保留
通过检查“与”操作结果和掩码相同,还是被擦除成0,我们能确切知道每一位的值是1还是0。然后通过对掩码做左位移 << 操作,产生针对每一位检测掩码。
00000000000000000000000010101010 //演员170
00000000000000000000000000000001 //掩码只有最低位是1
--------------------------------
00000000000000000000000000000000 //170最低位是0,掩码被擦除。结论:演员170的最低位是0。
左位移 << 操作
00000000000000000000000010101010 //还是演员170
00000000000000000000000000000010 //掩码只有次低位是1
--------------------------------
00000000000000000000000000000010 //这次掩码被保留。结论:演员170的次低位是1。
左位移 << 操作
00000000000000000000000010101010 //怎么又是演员170
00000000000000000000000000000100 //掩码倒数第三位是1
--------------------------------
00000000000000000000000000000000 //掩码又被擦除。结论:演员170的倒数第三位是0。
以此类推
下面是代码(我写得丑,对不起大家):
//Exercise 5:same as exercise 10 in chapter 3
public static void bitwise(){
//original number
final int NUM1 = 0xaa;
final int NUM2 = 0x155;
//print original number
//System.out.println(Integer.toBinaryString(NUM1));
//System.out.println(Integer.toBinaryString(NUM2));
//bitwise operate
int bitwiseAnd = NUM1 & NUM2; //与:某一位上,都是1,才输出1。
int bitwiseOr = NUM1 | NUM2; //或:某一位上,只要有1,就输出1。
int bitwiseXor = NUM1 ^ NUM2; //异或:两个里,一个0,一个1,才输出1。
int bitwiseNot = ~NUM1; //非:每一位取反,1变0,0变1。
//print bitwise result
System.out.println(Integer.toBinaryString(bitwiseAnd));
System.out.println(Integer.toBinaryString(bitwiseOr));
System.out.println(Integer.toBinaryString(bitwiseXor));
System.out.println(Integer.toBinaryString(bitwiseNot));
//print by my method
ControlFlow.printBinaryInt(bitwiseAnd);
ControlFlow.printBinaryInt(bitwiseOr);
ControlFlow.printBinaryInt(bitwiseXor);
ControlFlow.printBinaryInt(bitwiseNot);
}
//method that print binary string of int, Similar to Integer.toBinaryString()
public static void printBinaryInt(int inNum){
//bitwise mask
int mask=1;
//result container
int[] myInt = new int[32];
// 1. do "AND" operate
// 2. compare the result with the mask, to detect the value of each bit
// 3. left-shift the mask
for(int i=31;i>=0;i--){
int bitwiseResult = inNum & mask;
myInt[i]= bitwiseResult == 0 ? 0 : 1;
mask <<= 1;
}
//if is positive: dont print the highest bit.
//if is negative: print all 32 bit.
if (myInt[0]==0) {
//seek to first 1, and print the reste
int firstNoZero=0;
while(firstNoZero<=31 && myInt[firstNoZero]==0){
firstNoZero++;
}
if (firstNoZero!=32){
for(int i=firstNoZero;i<=31;i++){
System.out.print(myInt[i]);
}
} else {
System.out.print("0"); //the number is 0
}
} else {
for(int i=0;i<=31;i++){
System.out.print(myInt[i]);
}
}
System.out.println("");
}
output:
//系统Integer.toBinaryString()
0
111111111
111111111
11111111111111111111111101010101
//我的printBinaryInt()
0
111111111
111111111
11111111111111111111111101010101
//总算可以去吃饭了,好饿。
for 语句
多个参数控制for
Java的for语句的循环控制,允许有任意数量个变量参与,但所有变量必须是同一类型。不是单纯的for(int i = 1; i < 5; i++)这么简单。比如,如下的代码,用了i和j同时控制循环操作。
//书里的例子
for(int i = 1, j = i + 10; i < 5; i++, j = i * 2) {
System.out.println("i = " + i + " j = " + j);
}
for (element : collection)
for语句的另一种用法,for (element : collection){ }。这和python里的for element in collection:很像,都是执行遍历collection里的每一个元素。但语法上,显得没有python这么像在说话。
//语法
for (element : collection){ }
//栗子
int i[] = {1,2,3,4,5};
for(int x : i) {
System.out.println(x);
}
for的这种用法有个名称,叫for each语句。但要注意,for each只对数组,以及实现了Iterable接口的类有效。对于不能用for each语句的数据类型,作者在书里给出了一个重载range()方法的替代方案:for(object x : range()),但这需要我们自己重载range()函数。
break, continue以及标签
break和continue
前面讲过了,编程循环控制,比较常用的有for和while,他们都可以自带步进和终止条件。但同样的目的也可以用break,和continue来达到。而且更实用,控制更精细。
outer-iteration {
inner-iteration {
//.1.
break; //跳出inner-iteration,回到outer-iteration。
//.2.
continue; //不进行操作3,重新回到inner-iteration起始处。
//.3.
}
}
标签
标签相当于C语言里臭名昭著的goto语句。Java里没有goto关键字,但可以用标签来实现。具体的语法就是在迭代语句之前加上一行lablename:(注意标签和循环语句之间不能有任何其他语句)。这样当break和continue后面指定某个标签就能跳出循环,到指定标签位置。Java禁止在标签和循环语句中加内容,实际是为了保证代码的安全。
lable1:
//!!!注意:lable和循环语句之间,不能有任何内容!!!
outer-iteration {
inner-iteration {
//.1.
break lable1; //跳出inner-iteration和outer-iteration,到lable1的位置。再也不回到两个迭代中。彻底终止。
//.2.
continue lable1; //跳出inner-iteration和outer-iteration,到lable1的位置。然后从这里再进到outer-iteration和inner-iteration。
//.3.
}
}
下面书上给的这个例子很好,有点乱,但真的梳理清楚,就对break,continue,和标签的概念了解了。
public class LabeledWhile {
public static void main(String[] args) {
int i = 0;
outer:
while(true) {
print("Outer while loop");
while(true) {
i++;
print("i = " + i);
if(i == 1) {
print("continue");
continue;
}
if(i == 3) {
print("continue outer");
continue outer;
}
if(i == 5) {
print("break");
break;
}
if(i == 7) {
print("break outer");
break outer;
}
}
}
}
}
这个程序的输出会是怎么样的呢?等灯等灯,
i=0 continue
inner i=1
continue inner
i=2 continue
i=3 break
i=4 continue inner
i=5 continue inner
i=6 continue inner
i=7 continue outer
i=8 break outer
!!!注意: 一定要注意,只有当代码中有连环套嵌的循环语句的时候,才用标签lable。千万不要滥用!
练习 7
Modify Exercise 1 so that the program exits by using the break keyword at value 99. Try using return instead.
//exercise 7: print number,using break, and return
//这里用lable1只是为了实践一下。这种单层循环,无套嵌的情况不应该使用lable。
public static void oneToHundredBreak(int breakPoint){
int i=0;
lable1:
//lable和循环语句中间,不能插东西!!!
while(true){
if (i > breakPoint){
break lable1;
//return; //同效
}
System.out.println(i);
i++;
}
System.out.println("Out of loop!");
}
switch
java的switch语法长这样:
switch(integral-selector) {
case integral-value1 : statement; break;
case integral-value2 : statement; break;
case integral-value3 : statement; break;
case integral-value4 : statement; break;
case integral-value5 : statement; break;
// ...
default: statement;
}
练习 8
Create a switch statement that prints a message for each case, and put the switch inside a for loop that tries each case. Put a break after each case and test it, then remove the breaks and see what happens.
早上起床,诗兴大发:
//exercise 8: switch statement
public static void switchPoetry(int whichNumber){
for (int i=0;i<whichNumber+1;i++){
switch(i) {
case 1: System.out.println("一别之后"); break;
case 2: System.out.println("两地相悬"); break;
case 3: System.out.print("只说是三"); break;
case 4: System.out.println("四月"); break;
case 5: System.out.print("又谁知五"); break;
case 6: System.out.println("六年"); break;
case 7: System.out.println("七弦琴无心弹"); break;
case 8: System.out.println("八行书无可传"); break;
case 9: System.out.println("九连环从中折断"); break;
case 10: System.out.println("十里长亭望眼欲穿"); break;
case 100: System.out.println("百相思"); break;
case 1000: System.out.println("千系念"); break;
case 10000: System.out.println("万般无奈把君怨"); break;
}
}
}
output
//到5:ControlFlow.switchPoetry(5);
一别之后
两地相悬
只说是三四月
又谁知五
//到一万:ControlFlow.switchPoetry(10000);
一别之后
两地相悬
只说是三四月
又谁知五六年
七弦琴无心弹
八行书无可传
九连环从中折断
十里长亭望眼欲穿
百相思
千系念
万般无奈把君怨
练习 9
A Fibonacci sequence is the sequence of numbers 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on, where each number (from the third on) is the sum of the previous two. Create a method that takes an integer as an argument and displays that many Fibonacci numbers starting from the beginning, e.g., If you run java Fibonacci 5 (where Fibonacci is the name of the class) the output will be: 1, 1, 2, 3, 5.
Fibonacci很著名的作业题了。上学的时候调教了她好多次(。・`ω´・)。顺便再复习一下递归。
/**
* Fibonacci
* @author wei.shen@iro.umontreal.ca
* @version 1.0
*/
package com.ciaoshen.thinkinjava.chapter4;
import java.util.*;
/**
* This class contain different method to calculate Fibonacci number.
*/
public class Fibonacci {
/**
* some initial fields of the Fibonacci class
*/
//CONSTANT: fibonacci need two "1" at the beginning
private static long HEADONE = 1L;
private static long HEADTWO = 1L;
//container of fibonacci result
private static List<Long> fibonacciList = new ArrayList<Long>();
//我犯的一个错,<T>泛型里必须是对象,不能是基本型
//private static List<int> fibonacciList = new ArrayList<int>();
//we can also put this section into the constructor.
static{
fibonacciList.add(HEADONE);
fibonacciList.add(HEADTWO);
}
//default constructor
public Fibonacci(){ }
//print the fibonacci list
public static void print(List<Long> inList){
//for print comma
boolean isFirstNum=true;
for(long ele : inList){
if(!isFirstNum){
System.out.print(", ");
} else {
isFirstNum=false;
}
System.out.print(ele);
}
System.out.println("");
}
//the traditional iteration
public static List<Long> iterFibo(int howMuch){
//if not enough number, get the next one
for(int i=2;i<howMuch;i++){
//sum the last two number
long newNum = fibonacciList.get(fibonacciList.size()-2)+fibonacciList.get(fibonacciList.size()-1);
//insert into result list
fibonacciList.add(newNum);
}
return fibonacciList;
}
//the traditional recuresion
public static List<Long> recurFiboFast(int size){
//base case
if (size==1) {
List<Long> oneFiboList = new ArrayList<Long>();
oneFiboList.add(1L);
return oneFiboList;
} else if (size==2) {
List<Long> twoFiboList = new ArrayList<Long>();
twoFiboList.add(1L);
twoFiboList.add(1L);
return twoFiboList;
} else {
//go deeper: single line
List<Long> lastFiboList = recurFiboFast(size-1);
//go back: add the new number
long number1 = lastFiboList.get(lastFiboList.size()-1);
long number2 = lastFiboList.get(lastFiboList.size()-2);
long newNum = number1+number2;
lastFiboList.add(newNum);
//return
return lastFiboList;
}
}
/**
* main method
* @param args void
*/
public static void main (String args[]){
List<Long> testList1 = Fibonacci.iterFibo(10);
Fibonacci.print(testList1);
List<Long> testList2 = Fibonacci.recurFiboFast(10);
Fibonacci.print(testList2);
}
}
Output
//前5个:Fibonacci.iterFibo(5);
1, 1, 2, 3, 5
//100个?Fibonacci.iterFibo(100);
//Fibonacci成长曲线很快,90次左右,long型表示就受不鸟呢
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903, 2971215073, 4807526976, 7778742049, 12586269025, 20365011074, 32951280099, 53316291173, 86267571272, 139583862445, 225851433717, 365435296162, 591286729879, 956722026041, 1548008755920, 2504730781961, 4052739537881, 6557470319842, 10610209857723, 17167680177565, 27777890035288, 44945570212853, 72723460248141, 117669030460994, 190392490709135, 308061521170129, 498454011879264, 806515533049393, 1304969544928657, 2111485077978050, 3416454622906707, 5527939700884757, 8944394323791464, 14472334024676221, 23416728348467685, 37889062373143906, 61305790721611591, 99194853094755497, 160500643816367088, 259695496911122585, 420196140727489673, 679891637638612258, 1100087778366101931, 1779979416004714189, 2880067194370816120, 4660046610375530309, 7540113804746346429, -6246583658587674878, 1293530146158671551, -4953053512429003327, -3659523366270331776, -8612576878699335103, 6174643828739884737, -2437933049959450366, 3736710778780434371
简化代码?
其实我怒了,为什么我写的东西都这么肥大肥大肥大肥大。我就不能写个小一点的Fibonacci???????
public class Fibonacci {
public Fibonacci(){}
//just return the Nth fibonacci number
public static long fibo(int n){
if(n<=2){
return 1;
} else {
return fibo(n-1)+fibo(n-2);
}
}
public static void main (String args[]){
//just give me the next fibo quickly
for (int i=1;i<10;i++){
System.out.print (fibo(i)+" ");
}
}
}
亲,这个看上去很优雅,我喜欢(o>▽<)。但其实fibo()的效率比recurFiboFast()低多了。仔细看fibo()每层有两个分支,其中必定很多fibo数都是重复求的。如果层数多一点,血管马上爆。
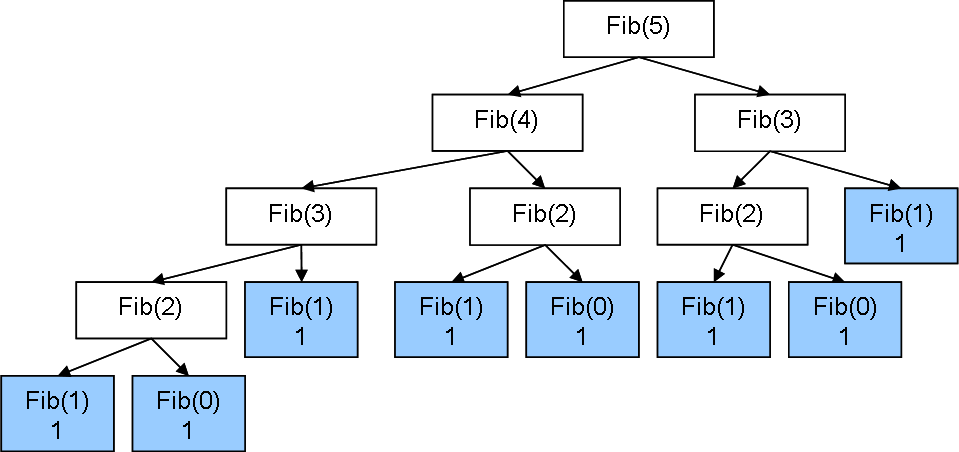
随便跑一个fibo(1)到fibo(200),我的MAC崩溃了。。。
但recurFiboFast(200)其实有点动态编程的影子,因为我把之前所有已经算出来的fibonacci数都存表里了,每次都只是去找表里的前两个值。复杂度是线性的,O(n)。
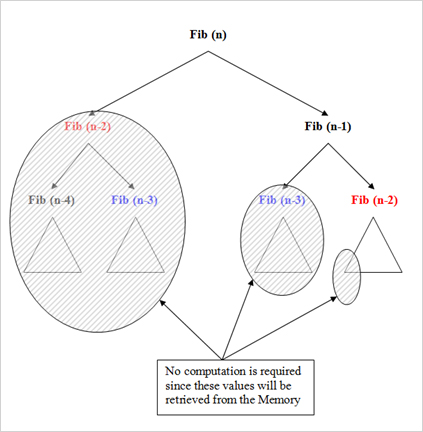
练习 10
A vampire number has an even number of digits and is formed by multiplying a pair of numbers containing half the number of digits of the result. The digits are taken from the original number in any order. Pairs of trailing zeroes are not allowed. Examples include: 1260 = 21 * 60 1827 = 21 * 87 2187 = 27 * 81 Write a program that finds all the 4-digit vampire numbers. (Suggested by Dan Forhan.)
因为特别特别特别饿,所以先写了一个最naive的暴力搜索,1000到9999一个一个拆开成两位数检查过去。而且代码有很多地方效率不高。吃完饭看看能不能简化代码,然后考虑有没有更优美的解法。
/**
* Vampire number
* @author wei.shen@iro.umontreal.ca
* @version 1.0
*/
package com.ciaoshen.thinkinjava.chapter4;
import java.util.*;
public class Vampire{
//default constructor
public Vampire(){ }
//only look for 4-digits vampire numbers
//丑陋暴力解法
public static List<Integer> getFourDigitsVampire(){
//the result container
List<Integer> resultList = new ArrayList<Integer>();
//for all 4-digits numbers
for(int currNum=1000;currNum<10000;currNum++){
//Pairs of trailing zeroes are not allowed.
if(currNum%100 != 0){
//permutations of ab*cd: P(4,2)*2
//2 nested loop
for(int digit1=0;digit1<4;digit1++){
for(int digit2=0;digit2<4;digit2++){
if(digit2!=digit1){
//call split(inNum,digit1,digit2)
// (abcd,1,3) --> {ac,bd}
// (abcd,2,4) --> {bd,ac}
List<Integer> halfHalf = split(currNum,digit1,digit2);
//check the pruduct
if(halfHalf.get(0)*halfHalf.get(1)==currNum){
if(!resultList.contains(currNum)){
resultList.add(currNum);
}
System.out.println(currNum+" = "+halfHalf.get(0)+" * "+halfHalf.get(1));
}
}
}
}
}
}
//return
return resultList;
}
// (abcd,1,3) --> {ac,bd}
// (abcd,2,4) --> {bd,ac}
public static List<Integer> split (int inNum, int digit1, int digit2) {
//result container
List<Integer> resultList = new ArrayList<Integer>();
//convert to digits
List<Integer> fourDigits=toDigits(inNum);
//get the rest number of digit1, digit2
List<Integer> restDigit = new ArrayList<Integer>();
for(int digit=0;digit<4;digit++){
if(digit!=digit1 && digit!=digit2){
restDigit.add(digit);
}
}
int rest1=restDigit.get(0);
int rest2=restDigit.get(1);
//get {ac,bd}
int part1=fourDigits.get(digit1)*10+fourDigits.get(digit2);
int part2=fourDigits.get(rest1)*10+fourDigits.get(rest2);
//insert into result container
resultList.add(part1);
resultList.add(part2);
//return
return resultList;
}
public static List<Integer> toDigits(int inNum){
//get 4 digital number
List<Integer> fourNum = new ArrayList<Integer>();
fourNum.add(0,(inNum%10000-inNum%1000)/1000);
fourNum.add(1,(inNum%1000-inNum%100)/100);
fourNum.add(2,(inNum%100-inNum%10)/10);
fourNum.add(3,inNum%10);
//return
return fourNum;
}
//to print the arraylist of integer
public static void printList(List<Integer> inList){
for (int ele : inList){
System.out.println(ele);
}
}
/**
* main method
* @param args void
*/
public static void main(String args[]){
//test split method
int myNum = 2016;
List<Integer> threeNumber = Vampire.split(myNum,1,3);
Vampire.printList(threeNumber);
//test getVampire
List<Integer> vampireResult = Vampire.getFourDigitsVampire();
System.out.println("Voila, here is our 4-digits vampire numbers: ");
Vampire.printList(vampireResult);
}
}
output
MacBook-Pro-de-Wei:java Wei$ sh run.sh Vampire
1260 = 21 * 60
1395 = 93 * 15
1435 = 41 * 35
1530 = 51 * 30
1827 = 21 * 87
2187 = 81 * 27
6880 = 86 * 80
6880 = 86 * 80
Voila, here is our 4-digits vampire numbers:
1260
1395
1435
1530
1827
2187
6880
天外有天
为什么我喜欢算法呢?因为她美。为什么美呢?因为你的解法永远不会是最美得那一个。为什么Dan Forhan会推荐这道题呢?因为果然这题明显洞天里面有洞天啊。
第二种解法,逆向思维。既然是两个两位数相乘,我们就可以遍历所有两位数,求积,再比较原数和积。这个比较可以用拆开排序的方法,因为只要求数字相同,顺序没关系。1260和2160拆开排序后都是0126。这其实也算暴力解法,只是和前面的方法相反的角度出发,但效率就要高一点。以下是代码:
public class Vampire{
//default constructor
public Vampire(){ }
//another method to get the 4 digits vampire number
public static List<Integer> getFourDigitsVampireV2(){
//result container
List<Integer> vampireList = new ArrayList<Integer>();
//nested loop: check each ab and cd
for(int part1=10;part1<100L;part1++){
for(int part2=part1;part2<100L;part2++){
int product = part1*part2;
if (!(product<1000 || product >= 10000 || product%100==0)){ //only need 4 digits number and those end with 00
//split to list of int 1234 -->{4,3,2,1}
List<Integer> origList = toInvertDigits(part1*100+part2);
List<Integer> productList = toInvertDigits(product);
//sort
Collections.sort(origList);
Collections.sort(productList);
//compaire the sorted list
if (origList.equals(productList)){
System.out.println("found "+part1+" * "+part2+" = "+product);
vampireList.add(product);
}
}
}
}
return vampireList;
}
//input:1234 --> output: {4,3,2,1}
public static List<Integer> toInvertDigits(int inNum){
List<Integer> resultList = new ArrayList<Integer>();
while(inNum>0){
resultList.add(inNum%10);
inNum/=10;
}
return resultList;
}
/**
* main method
* @param args void
*/
public static void main(String args[]){
//test getVampire
List<Integer> vampireResult = Vampire.getFourDigitsVampireV2();
System.out.println("Voila, here is our 4-digits vampire numbers: ");
Vampire.printList(vampireResult);
}
}
但以为这样就完了吗?too naive too simple。还是上Think in Java的官方答案吧。
同样是两层套嵌loop两位数10-99,然后关键在后面:
根据Pete Hartley的数学公式: 如果
x*y是吸血鬼数,那么x*y == x+y (mod 9)。
为什么会有人发现这样的外挂呢?我这辈子应该不可能是巨人的,看样子只能站在巨人的肩膀上了。
//: control/E10_Vampire.java
/****************** Exercise 10 *********************
* A vampire number has an even number of digits and
* is formed by multiplying a pair of numbers containing
* half the number of digits of the result. The digits
* are taken from the original number in any order.
* Pairs of trailing zeroes are not allowed. Examples
* include:
* 1260 = 21 * 60
* 1827 = 21 * 87
* 2187 = 27 * 81
* Write a program that finds all the 4-digit vampire
* numbers. (Suggested by Dan Forhan.)
****************************************************/
public class E10_Vampire {
public static void main(String[] args) {
int[] startDigit = new int[4];
int[] productDigit = new int[4];
for(int num1 = 10; num1 <= 99; num1++)
for(int num2 = num1; num2 <= 99; num2++) {
// Pete Hartley's theoretical result:
// If x·y is a vampire number then
// x·y == x+y (mod 9)
if((num1 * num2) % 9 != (num1 + num2) % 9)
continue;
int product = num1 * num2;
startDigit[0] = num1 / 10;
startDigit[1] = num1 % 10;
startDigit[2] = num2 / 10;
startDigit[3] = num2 % 10;
productDigit[0] = product / 1000;
productDigit[1] = (product % 1000) / 100;
productDigit[2] = product % 1000 % 100 / 10;
productDigit[3] = product % 1000 % 100 % 10;
int count = 0;
for(int x = 0; x < 4; x++)
for(int y = 0; y < 4; y++) {
if(productDigit[x] == startDigit[y]) {
count++;
productDigit[x] = -1;
startDigit[y] = -2;
if(count == 4)
System.out.println(num1 + " * " + num2
+ " : " + product);
}
}
}
}
}